1617. Разрушение дорог
Между каждой
парой городов страны имеется прямая двусторонняя дорога. Петр хочет взорвать
такое количество дорог, чтобы образовалось хотя бы два города, проезд между
которыми был невозможен.
Вам известна
стоимость подрыва каждой дороги. Найти наименьшую стоимость, за которую Петру
удастся совершить задуманное.
Вход. Состоит из нескольких тестов. Первая строка каждого теста
содержит количество n (n ≤ 50) городов в стране.
Следующие n строк описывают дороги: j-ый символ i-ой строки является цифрой, задающей стоимость уничтожения дороги,
ведущей из i-го города в j-ый.
Выход. Для каждого
теста вывести в отдельной строке наименьшую стоимость, за которую Петру удастся
совершить задуманное.
|
Пример
входа |
Пример
выхода |
|
4 0911 9011 1109 1190 6 030900 304120 040174 911021 027207 004170 4 0399 3033 9309 9390 |
4 8 9 |
РЕШЕНИЕ
максимальный
поток
Анализ алгоритма
Рассмотрим граф,
в котором города являются вершинами, а двусторонние дороги – неориентированными
ребрами. По условию задачи в графе необходимо удалить такое множество ребер,
суммарная стоимость которых наименьшая. Это классическая задача о минимальном
разрезе. В то же время известно, что минимальный разрез графа равен
максимальному потоку. Для любого разреза нулевая вершина будет отделена от
какой-нибудь другой. Поэтому находим максимальный поток между нулевой и i - ой (0 < i < n = |V|) вершиной
и среди всех значений найденных потоков находим наименьшее.
Пример
Рассмотрим
первый тест. Максимальный поток между вершинами 0 и 2 равен 4. Путями, по
которым будет двигаться поток величины 4, будут:
·
0 – 1 – 2, поток величины 1;
·
0 – 2, поток величины 1;
·
0 – 3 – 2, поток величины 1;
·
0 – 1 – 3 – 2, поток величины 1;
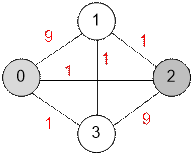
В то же время
·
максимальный поток между вершинами 0 и 1 равен 11;
·
максимальный поток между вершинами 0 и 3 равен 4;
Реализация алгоритма
Объявим рабочие
массивы. cap[i][j] содержит стоимость уничтожения дороги между i-ым и j-ым городом.
#define MAX 50
int cap[MAX][MAX], res[MAX][MAX],
used[MAX];
Функция aug(x, t,
CurFlow) находит пропускную
способность дополняющего пути от вершины x
до t, если известно, что пропускная способность
дополняющего пути от начальной вершины до x
равна CurFlow.
int aug(int
x,int t,int
CurFlow)
{
if (x == t) return CurFlow;
if (used[x]++) return
0;
for (int Flow, y = 0; y < n; y++)
{
if
(res[x][y] > 0 && (Flow = aug(y,t,min(CurFlow,res[x][y]))))
{
res[x][y] -= Flow; res[y][x] += Flow;
return
Flow;
}
}
return 0;
}
Функция mincut(s, t) находит величину
максимального потока между вершинами s
и t.
int mincut(int
s, int t)
{
memcpy(res, cap, sizeof(cap));
int x, flow =
0;
do
{
memset(used,0,sizeof(used));
} while ((x =
aug(s,t,0x7FFFFFFF)) && (flow += x));
return flow;
}
Вычисляем максимальный поток от
нулевой вершины до s-ой (1 ≤ s ≤ n – 1). Среди найденных максимальных потоков ищем минимальный.
int requiredCost(void)
{
int best =
0x7FFFFFFF;
for (int s = 1; s < n; s++)
best = min(best,mincut(0, s));
return
best;
}
Основная часть программы. Читаем
данные для каждого теста и вызываем функцию requiredCost.
while(scanf("%d\n",&n)
== 1)
{
for (i = 0; i
< n; i++)
{
gets(s);
for (j = 0;
j < n; j++)
cap[i][j] = s[j] - '0';
}
printf("%d\n",requiredCost());
}
Реализация алгоритма – bfs, Эдмондс - Карп
#include <iostream>
#include <string>
#include <queue>
#include <cstring>
#include <algorithm>
#define MAX 50
#define INF 0x3F3F3F3F
using namespace std;
int cap[MAX][MAX], m[MAX][MAX],
used[MAX], parent[MAX];
int i, j, n;
string s;
void bfs(int v, int final)
{
queue<int>
q;
q.push(v);
used[v] = 1;
while
(!q.empty())
{
int from
= q.front(); q.pop();
if
(from == final) return;
for (int to =
1; to <= n; to++)
if
((m[from][to] > 0) && (!used[to]))
{
used[to] = 1;
parent[to] = from;
q.push(to);
}
}
}
void Rebuild(int k, int flow)
{
if
(parent[k] == -1) return;
Rebuild(parent[k], flow);
m[parent[k]][k] -= flow;
m[k][parent[k]] +=
flow;
}
int FindFlow(int k)
{
if
(parent[k] == -1) return INF;
int x =
FindFlow(parent[k]);
return
min(x, m[parent[k]][k]);
}
int Flow(int source, int final)
{
memcpy(m,
cap, sizeof(cap));
int
MaxFlow = 0;
while (1)
{
memset(parent,
-1, sizeof(parent));
memset(used,
0, sizeof(used));
bfs(source, final);
int flow
= FindFlow(final);
if
(flow == INF) break;
MaxFlow
+= flow;
Rebuild(final,
flow);
}
return
MaxFlow;
}
int requiredCost(int n)
{
int res
= INF;
for (int s =
1; s < n; s++) // vertices 0..n-1
res =
min(res, Flow(0, s));
return res;
}
int main(void)
{
while (cin
>> n)
{
memset(cap,
0, sizeof(cap));
for (i =
0; i < n; i++)
{
cin >> s;
for (j =
0; j < n; j++)
cap[i][j] = s[j] - '0';
}
printf("%d\n",
requiredCost(n));
}
return 0;
}